paired observations: Two observations considered to be related to each other.

2. Two sets of equal number of observations with a bijection between the 2 sets.

pair set: The formation of a new set that consists of two elements of a set (or two sets) only, with no other members.

pair-wise disjoint: The property of a collection of mathematical objects, any two of which have a null (empty) intersection.

Pappus’s theorem: A number of theorems attributed to Pappus of Alexandria including the Pappus's Centroid Theorems which intuitively states that the area of a surface of revolution can be calculated by finding the product of an arc length and the length travelled by its centroid and the volume of a revolution definied by a curve f can similarly be found by finding the product of the area under f and the length travelled by its centroid.

Parabola: The shape formed by the intersection of the conical surface of an infinite cone and a plane that is "parallel" to a generatrix of the cone. (The plane is parallel to a line in the sense that any normals to the plane is perpendicular to the line.) As a conic section, it has an eccentricity of exactly 1. The plural form of parabola is parabolae.

An alternative definition defines the locus of all points that is equidistant from a point known as the focus, and a line known as the directrix. A parabola is specified as long as the focus does not lie on the directrix.

All parabolae are effectively of the same shape (with eccentricity 1), being scaled versions of other parabolae. Also, all parabolae are symmetirc about the normal of the apex (vertex).

 

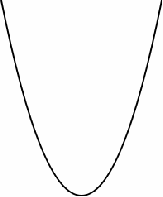
parabolic: Of or related to the shape of the parabola.

parabolic spiral: Also known as Fermat's spiral, a spiral defined by the relationship between the radius and argument of a point in polar coordinates such that the radius is proportional to the square root of the argument.

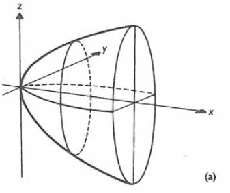
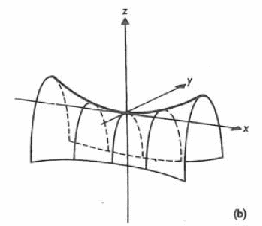
Paraboloid: A couple of related family of shapes formed by parabolae. An elliptic paraboloid, the figure as shown below on the left, is the surface of revolution of a parabola about its axis of symmetry. While a hyperbolic paraboloid, as shown on the right, can be formed by "stacking" a number of identical parabolae such that the collection of the vertices of the parabolae themselves form a parabola.

paradox: The situation where valid inferences made on valid premises seemed to imply a contradiction. Note that the mathematical (logical) definition of a paradox is much narrower than in everyday use.

parallel: Describing lines (or other geomtric objects) that are non-intersecting, "going" in the same direction and keep equal distance everywhere. For lines, these three concepts are exactly the same in Euclidean geometry, while in other geometries, the concept of parallel (without further clarifications) can be taken to mean an extension to any of these, given that this concept on geometric objects originated from related concepts that happen to be the same in Euclidean geometry.

parallelepiped: A polyhedron consisting of 6 faces (3 pairs of identical parallelograms), 12 edges (3 sets of 4 parallel lines) and 8 vertices. They are related to parallelograms as cuboids are to rectangles. Or equivalently, they are related to cuboids as parallelograms are to rectangles. (i.e. a parallelopiped is a "slumped" cuboid.)

parallelogram: A quadrilateral formed by two pairs of parallel edges of equal length.

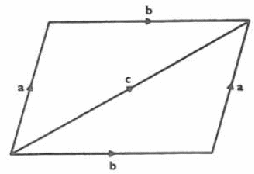
parallelogram law: A law that states the commutativity of addition of vectors. In simple words, given any vectors a and b, a + b = b + a. It is so called because it can be illustrated graphically by a parallelogram as below.

parallel postulate: An assertion by Euclid in his book Elements. It was presented as a postulate (after 4 others) without being proven. It effectively states that two non-parallel lines must meet.

This "postulate" has resisted proof for many centuries before consideration is given to the possibility that it is simply not necessarily true. This leads to the development of non-Euclidean geometry, while the familiar geometry in which the fifth postulate is true is known as Euclidean Geometry. It should be noted that we now know of the parallel postulate's independence from the other postulates, that is, the parallel postulate cannot be proven from the four other postulates. In that sense, the parallel postulate of Euclid is more of an axiom for a particular geometric system.

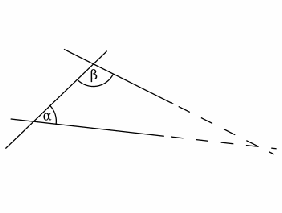
parameter: A variable (and by extension, a constant value that the variable takes) which determines (sometimes uniquely) the behaviour of a mathematical system such as an equation or an expression.

parametric equations: A way of describing relationships between variables through other variables known as parameters. For example, we may define the relationship between two variables x and y through a variable t, which we are not interested in. (i.e. we would not particularly want to plot a graph with x, y and t axis, but rather x and y axis only. The variable t is only present to facilitate the description of the relationship between x and y)

Some equations would be parametric simply because it is not easy (or is impossible) to be stated in ordinary (i.e. explicit or implicit) form. For example, x = 2^t + t² and y = t^t should be difficult to express without the parameter t or any other "intermediaries".

parametrisations: The act of expressing equations in parametric forms.

parent functions: A collection of simple functions used to build more complicated functions. In this sense there are no definitions of what constitue "simple" and is even more vague than the idea of elementary functions.

parentheses: Pairs of symbols ( ) used to indicate the priority in calculations that may break away from conventions (e.g. left to right, multiplications before additions), or provides information into the preferred grouping of multiple objects. (e.g. a x b x c for the vector triple product) Often known as brackets or round brackets.

parity: The state of a positive integers being odd or even. Determined by whether it is divisible by 2.

partial correlation coefficient: The coefficient of correlation between 2 random variables with all other random variables fixed.

partial derivative: The result when a function is differentiated with respect to one of its multiple arguments, while the other arguments are held fixed (considered as constants).

If in a geometric visualization, we think of an ordinary derivative as the function of the gradient of tangents of points on a curve, then a partial derivative can be thought of as a function of the gradient of a tangent of points on a surface, in the direction of the chosen argument.

partial differential equation: An equation expressed with partial derivatives. It is thus also a differential equation where the function concerned has multiple variables as arguments.

partial differentiation: Differentiation of a multivariate function with respect to only one of its several variable arguments.

partial fractions: A method of expressing an algebraic fraction as a sum of several simpler (i.e. lower degree) algebraic fractions. For example,

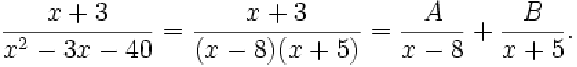
With A = 11/13 and B = 2/13.

partial quotient: A method of division also known as the chunking method.

partial sum: The sum of the first terms of a series. S_n = a₁ + a₂ + a₃ + ... + a_n

Usually the number of terms is specified and we must sum the first specified nuber of terms without omitting any. The concept of partial sums allow the definition of the convergence of a series to be based on that of a sequence. Examining the partial sums of a series also helps evaluate the sum of infinite sereis.

particle: In mechanics, the concept of an ideal object with position and mass (thus momentum and other concepts that follow) but no (or negligible) size and spin.

particular solution: A solution of a differential equation where the arbitrary constants take on particular values.

partition of an interval: The act of dividing an interval into a set of non-overlapping intervals that together complete cover the original.

pascal: An SI derived unit of pressure - the pressure of 1 Newton of force acting uniformly over 1 m² of area.

Pascal's triangle: A triangular array of numbers, with simple rules governing the generation of numbers in each new row, where the numbers are the binomial coefficients.

path: A sequence of vertices where any two consecutive vertices in the sequence are connected by an edge.

payoff matrix: A matrix which represents the payoffs in the study of game theory.

PDE: Partial differential equations. As opposed to ordinary differential equations (ODE).

pendulum: A mechanical construction where a weight suspends from a string or a rod whose other end is fixed to a point.

pentagon: A five-sided polygon.

pentahedron: A polyhedron with five faces, For example, a square pyramid.

per annum: A phrase meaning "per year" in Latin. Often used in financial contexts such as relating to interest rates.

percent: One part out of a hundred. Could be considered a dimensionless unit. It is often represented by the symbol %.

percentage error: A measure of error, taking in account the actual value, calculated by

percentile: A type of quantile, a point below which some whole number of percentage of data fall.

perfect number: A whole number which is equal to the sum of all its proper factors.

perfect square: Also known as a square number. A perfect square is the square of an integer.

pericycloid: A type of epicycloid where one circle completely circumscribe the other circle at all times, as the outer circle roll around the inner circle.

perigon: A angle, a full 360° turn.

perimeter: The length of a closed curve, commonly the edges and boundaries of a plane figure

period: The length of a minimal interval of argument of a periodic function that contains one full cycle.

period doubling: The increase of the period of a mathematical system to two-fold of the period prior to the change.

periodic decimal: Also known as repeating or recurring decimal.

periodic function: A function which repeats in such a way that, two arguments separated by a multiple of the period of the function are always the same. Important examples include the trigonometric functions as well as functions such as frac(x) = x - floor(x).

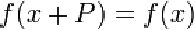
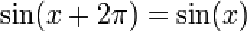
permutation: 1. Some form of rearrangement of the elements within a set.

2. The number of ways of choosing r elements from a set of n elements when the order of being chosen matter. This is the same as performing (the equivalent actions associated with) combination followed by the factorial.

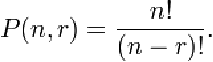
perpendicular: The state of geometric objects being at right angle to each other.

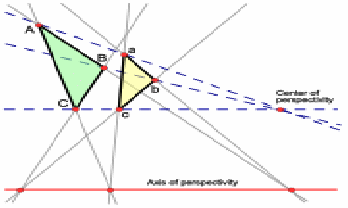
perspective: The point that is the intersection of all lines which run through corresponding vertices of 2 plane figures. Note that for plane figures which are mathematically similar, the centre of enlargement is the perspective.

phase: The position within a cycle for a periodic system. Due to the nature of periodic systems there is usually no "natural" starting point of a cycle and one would be needed as a reference point most of the time to quantify the phase.

pi: A transcendental number (thus irrational number) that is the ratio of the length of circumference to the length of the diameter for all circles. Owing to it being a transcendental number, there is no easy way to express the number without sacrificing accuracy, thus we commonly use the greek letter pi, π, to represent this number. The importance of this number grows beyond circles as it appears in number theory and probability. While, with the help of modern computers and efficient algorithms, we currently know this number to over a trillion digits, we shall need no more than 100 decimal places for calculating circles that fit within the largest of space that we know (the observable universe) for an accuracy smaller than anything that we know (planck length).

π(x): A function whose value is the number of prime numbers less than or equal to x.

pictogram: In graphical representation of data in statistics, where pictures are used.

piecewise continuous: A function which is continous at all points except for a finite number of points, which are the "boundaries" of the pieces.

pie chart: A form of representation of qualitative (or discrete categories of) data. Useful in representing the frequency of a category presented as relative to the overall total.

piercing point: The point where a curve/surface intersects with the coordinate axes.

pinching theorem: Also known as the Squeeze theorem. A theorem that states that, if a function is known to be less than or equal to (or alternatively, more than or equal to) a function, then its limit shall also be less than or equal to (or correspondingly, more than or equal to) the limit of the bounding function. In one application, finding two functions (one bounding above and one below) with the same limit forces the squeezed function to have the same limit as the other two.

pint: An British Imperial unit of volume equal to an eighth of a (British Imperial) gallon or 20 (Bitish Imperial) fluid ounces.

planar graph: In graph theory, a graph that can be represented on a plane without any intersection of its edges. Note that a planar graph is an inherent property of the graph invariant to its representation while a plane graph refers to the representation in a plane.

plane: A set of points which can be defined by (but not uniquely) the location of a point (on the plane), and two directions (parallel to the plane but not parallel to each other).

plane geometry: The study of geometry within a plane.

plane of symmetry: The plane that is the collection of invariant points under a reflection such that the overall shape (or any collection of points) also stays invariant.

plane section: The collection of points that is the intersection of a plane with another geometric object of 3 or more dimensions.

plane trigonometry:The study of triangles (trigonometry) within a plane.

platonic solids: A convex regular polyhedron - regular in the sense that a linear transformation of any vertex to any other vertex of the polyhedra, such that an edge adjacent to the originating vertex coincides with an edge adjacent to the destinating edge will ensures that all other vertices and edges also coincide with another vertex/edge respectively.

plus/minus sign: The sign ± combining the two operations in two cases. Most commonly seen in the quadratic formula indicating two different solutions, one while the addition is used and one while the subtraction is used.

It is also seen in compound angle formulae in trigonometry for the convenient expression of pairs of related identities, where the minus/plus sign is also seen. In this case, the minus/plus sign serves the same function but correspond to the opposite cases. (i.e. When the "top" case is chosen, we use the addition in the plus/minus sign and the subtraction in the minus/plus sign, and when the "bottom" case is chosen, we use the subtraction in the plus/minus sign and the addition in the minus/plus sign.)

Also note that another common use of the sign to indicate a range (such as a confidence interval is not a strict mathematical use. 45% ± 3%.

plus sign: A symbol used to denote addition.

point: An ideal object in geometry of zero dimensions.

point estimate: The estimate of a (unknown) value by giving a value. As opposed to an interval estimate.

point of contact: The point where a tangent meets a curve so that they can be considered parallel at the point of intersection.

point of inflection:Also known as inflection, inflection point, inflexion or inflexion point (alternative spelling of inflection).

point-slope form: A particular way of representing the equation of a straight line such that a point on the line and the slope of the line can be easily extracted from the equation with no calculations.

Poisson distribution: AThe discrete probability distribution of the number of independently singly events over a fixed "length" (of space or time or similar continua) given a constant rate.

The probability mass function is given by.

 

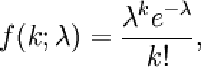
where "lambda" is the constant rate within the given length of the interval, while k is the number of singly events occurring within such an interval.

polar angle: The angle that the line segment joining a point and the pole makes with the initial axis in a polar coordinate system.

polar axis: Also known as the initial axis. The axis usually considered to coincide with the positive x-axis. A reference axis within the polar coordinate system.

polar coordinate system: A 2-dimensional coordinate system where the location of a point is specified by its distance from the pole (radius) as well as the polar angle. A polar coordinate system may simplify the description of certain types of curves such as circles or spirals.

 

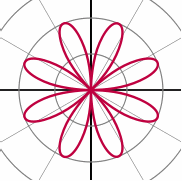
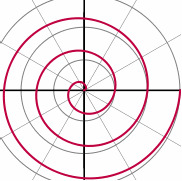
polar equation: An equation of a curve expressed in radius and polar angle of the polar coordinates system.

polar form: Also known as the modulus-argument form of a complex number A represention of a complex number with its modulus and argument, essentially the radius and polar angle of a point within the polar coordinates system.

polar integral formula : The method of finding the area between a curve and the half-lines θ = a and θ = b through an integral of the equation describing the curve.

polar normal: The segment of normal between the contact point and the intersection of the normal with a line through the pole which is perpendicular to the radius of the contact point.

polar tangents: The segment of tangent between the contact point and the intersection of the tangent with a line through the pole which is perpendicular to the radius of the contact point.

polar triangle: A triangle which is bounded by the polars of a triangle's vertices with respect to a conic.

pole: The polar analogue of the origin in the Cartesian coordinate system.

polygon: A closed curve on a plane formed by more than one line segment. (Which also entails that there are more than two line segments, thus a triangle is a polygon with the minimal number of sides.)

A polygon can be classified as equilateral (all sides are of the same length), equiangular (all angles are the same), regular (both equiangular and equiangular) or none of the above. It can also be independently classified into convex (all interior angles are less tha 180°) or concave (at least one angle is reflex - more than 180°).

A 3-dimensional analogue is called a polyhedron.

polygon of forces: A generalisation of the triangle of forces where there are 2 or more forces being combined together by vector addition and the result is represented as a polygon.

polyhedral angle: The geometrical construction of the neighbourhood of a vertex bounded by the vertex itself, 3 or more edges from the vertex, as well as the same number of faces (as edges) between the edges.

polyhedron: A 3 dimensional object bounded by 2-dimensional surfaces which are polygons. It is essentially the 3-dimensional analogue of a polygon.

polynomial: A polynomial is a mathematical expression that is the sum of a finite number of terms, each being either a constant term or the product of a constant and a positive integer power of a variable.

p(x)=a_n xⁿ + a_n-1 x^n-1 + ... + a₂ x² + a_a x + a₀

The terms are identified by the power that the variable is raised to and the corresponding constant in the term is known as a coefficient of that term.

The leading coefficient of a polynomial is the coefficient of the term of highest power in a single variable case. (It is "leading" due to the convention of writing finite number of terms in descending order, this leading coefficient often determines the golbal behaviour of the polynomial.)

Polynomials of lower orders have special class="d-title" names: a polynomial of highest power of 1 is linear, 2 is quadratic, 3 is cubic, 4 is quartic and 5 is quintic. Special class="d-title" names are seldom used in powers higher than 5.

polytope: A generalisation of polygons and polyhedra to all dimensions.

population: The set of members under study where samples are taken.

positional system: A system representing numbers where symbols can take on different (but usually related) meanings depending on its (relative) position within the collection of symbols.

position vector: A vector used to represent the position of a point via the relative position of this point to a known reference universal within the coordinate system, such as the origin 0. Often denoted by the symbol r.

positive angle: A plane angle taken to be anti-clockwise from some reference axis.

positive definite: The property of a real symmetric square matrix M such that z^TMz > 0 for all non-zero column n-vectors z. 

 

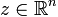
, where z^T represents the row vector which is the transpose of z.

positive number: Any number greater than zero. Note that this definition would only apply if such a comparison could be made. (For example, while one of the three statements a < b , a = b , a > b must be true for real numbers, it is not the case for complex numbers, thus the concept of "greater than" and by extension "positive" may not make sense.)

Note also that the set of positive numbers is slightly different from the set of non-negative numbers. (Mainly because even a real number can be neither positive or negative.)

positive semi-definite: The property of a real symmetric square matrix M such that z^TMz ≥ 0 for all non-zero column n-vectors z. 

 

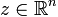
, where z^T represents the row vector which is the transpose of z.

positive series: A real series consisting only of positive terms.

postulate: Can be taken to mean an axiom, although some maintain a distinction between the two. Although there may not be any consenses in such distinctions.

potential: For electrical potential, work per unit charge. See potential energy.

potential energy: Energy stored in an object (or a system) due to the position of the object (or the physical configuration of the system).

pound: Imperial unit of mass equivalent to roughly 5/11 of a kilogram..

power: Also known as exponent or index. The number of base number to repeated multiply (and subsequent extensions of this definition).

power series: Any infinite series which takes the form

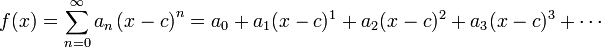
precision: The reciprocal (multiplicative inverse) of the variance of a sample or a population.

predicated variable: Also known as independent variable, explanatory variable amongst other class="d-title" names. Not to be confused with predicate variables in first-order logic.

predictor variable: Another class="d-title" name for an independent variable, explanatory variable or a predicated variable.

prefix notation: Also known as Polish notations, where the operator is expressed before the operands. Such a system has as its advantage simpler structure requiring very few brackets (or none at all), but may cause confusion unless other ways are used to indicate multiplication, such as 2x to mean the product of 2 and x, and for the positional system of representing numbers where 34 means the sum of thirty and four.

pre-image: A subset of the domain that corresponds to a given subset of the codomain.

pressure: The measure of force exerted over a standardised area. Often denoted with the Greek letter p (rho). The S.I. unit of pressure is the Pascal (class="d-title" named after Blaise Pascal), being the equivalent of one Newton with a square metre.

primality: The state of a positive integer being a prime number.

prime (prime number): A positive integer with exactly 2 factors. (Where 1 is necessarily one of the factors and itself another.) While 1 has been considered a prime number at times it is usually not by the aforementioned modern deion.

prime factorisation: The breaking down of an integer into prime factors. The fundamental theorem of arithmetic guarantee that the factorisation of an integer is unique regardless of the way of factorisation.

prime number theorem: A theorem which gives some information on the distribution of prime numbers.

prime pair: Consecutive prime numbers - ones which differ by exactly 2, also known as twin primes.

prime symbol: Also known as the accent or simply "dash". Usually placd on the top right of other mathematical symbols to indicate derivatives such as f'(x), related objects such as point p and p' or arbitrary constant C and C', measurements such as feet and minutes (angles).

primitive curve: A simple curve with which (upon which) a more complicated curve can be comapred (defined).

primitive polynomial: A polynomial with coefficients which share no common divisors (one which divides all coefficients).

primitive root: The "principal" root of a complex number. Usually chosen to be the complex number with the least positive argument.

principal: The amount of money on which interest payments calculations are based on.

principal diagonal: Also known as the main diagonal. The diagonal running from top left to bottom right in a matrix. (The diagonal with the elements 1 in an identity matrix.)

principal directions: The direction of one of the principal curvatures of a surface.

principal parts: The part of the increment of the value of a function (curve) as approximated by the derivative (gradient) and the increment in the argument.

principal value: The value chosen as the value of the function that approximates the inverse of a many-to-one function. i.e. the many-to-one function restricted to the domain of the principal values is a one-to-one function (bijection).

principle of moments: The assertion that the clockwise and anti-clockwise moments about the same point (which may or may not be the pivot) are the same for objects in equilibrium.

prism: A solid figure whose cross section (perpendicular to an axis) is the same along the whole axis.

prismatoid: The generalisation of a prism - a solid figure formed by vertices which lie in either one of 2 parallel planes.

Prismatoid formula: The formula for calculating the volume of a prismatoid derived from the Simpson's rule.

prisoner's dilemma: A family of related symmetric decision making problems with 2 players in game theory where the Nash equilibrium is not the optimal state for either player.

probability: A quantitative measure of the likelihood of an event's occurrence, taking a value between 0 and 1 (inclusive).

probability density function: See fThe function that describes the probability density (the quantity whose product with the length of the interval is probbility) for continuous probability distributions.

probability distribution: A function of a discrete variable whose integral over any interval is the probability that the random variable specified by it will lie within that interval

probability function: Often known as the probability mass function. Although stated as such it can be taken to mean the cumulative distribution function as well.

probability generating function: A representation of the probability mass function of a discrete random variable by the terms of a power series.

probability mass function: The function the computes the probability for an event for a discrete probability distribution.

probability paper: A type of graph paper where the scales on the axes are manipulated such that a certain distribution represents a straight line on the paper such that it makes for easier fitting of data to the specified distribution.

produce: Extending a line.

product: The result of multiplication or any operations on mathematical objects deemed close enough in resemblence to multiplication. (Such as the scalar product and the vector product in vectors.)

product formulae: A number of trigonometric identities resulting from exploiting the similarity in form for compund angle formulae in the addition and subtraction cases. (Since both sides of the identity differ only by one sign.)

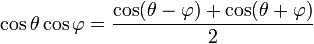
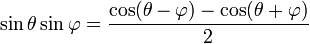
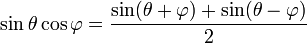
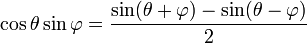
product moment: One way of calculating a coefficient of correlation known as the Pearson's product-moment correlation coefficient.

product rule: A theorem in differentiation that provides an easy way to differentiate the product of two functions. It can be easily proven from first principles and can be easily extended to cases covering the product of three or more functions. It is also easy enough to remember for most without resorting to commiting the following symbols to memory.

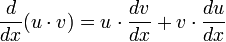
programming: Mathematical optimisation.

progression: 1. An older term for a sequence.

2. A sequence where each term is determined by a fixed (simple) rule and the preceeding term.

projectile: An object purturbed from stationary by a force before being subjected to air resistance and gravity only - where the effects of air resistance is generally understood to not reduce the speed of the object.

projection: Along a line, a mapping that identifies all points on the line to be the same point and applying the same to all lines parallel to the original line.

prolate spheroid: A sphere stretched along one axis. (Squashing along one axis or stretching along perpendicular axes make a oblate spheroid.)

proof: A sequence of finite number of statements, each of which is either an axiom or the result from rules of inference on statements that appeared before.

proof by contradiction: A method of proof based on the fact that a logical sentence and its contrapositive always hold the same truth value. One attempts to prove a sentence by contradiction by assuming the inverse of the desired statement and shows that it must lead to some logical contradiction. Thus, "if the negation of the original statement leads to a contradiction means no contradiction arises leads to the original statment being true.".

proof by contraposition: A method of proof where we proof a statement by its (necessarily logically equivalent) contrapositive.

proper divisor: A non-trivial factor (i.e. divisor). The trivial factors are 1 and the number itself, since they are always factors regardless of the number being divided.

proper fraction: A fraction whose numerator is strictly less than the denominator. The same concept can be extended to cover algebraic (rational ) fractions by insisting that the order of the polynomial in the numerator be less than the order of the polynomial in the denominator.

properly divergent: The property where the terms (of a sequence) or the partial sums (of a series) is unbounded - thus necessarily divergent.

proper subset: A proper subset is one completely contained within another. X is a proper subset of Y is al elements of X are elements of Y (this qualifies X as a subset of Y), and there is at least one element of Y that is not in X. (This qualifies for the "proper")

proportional: Describes the relationship between 2 quantities are such that they both change by the same factor (considered as multiplication).

p-series: The series that is the sum of the reciprocal of all postive integers raised to the power of p.

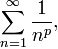
If p is 1 then the series is known as a harmonic series. This series is convergent for all x >1 and divergent otherwise.

pseudoprime: A composite number which shares some (prime related) properties of a prime number.

pseudo-random numbers: Numbers generated using an algorithm (thus deterministic) which approximates the desirable properties of a list of random numbers.

pulsatance: Angular frequency - known as pulsatance in specific contexts.

pure imaginary: A complex number containing no real part. (i.e. real part of value 0.) These are the numbers lying on the "other axis" (i.e. the one other than the real number line) in an argand diagram.

pure surd: A surd which is not also the product of an integer (other than 1) and another surd.

p-value: The probability that a test statistic take the value of, or more deviated than, the actual value observed. Intuitively speaking this calculates the probability that the observed result happens by chance rather than other reasons. We reject the null hypothesis if the p-value of an observed value of a test statistic is less than that of a pre-determined significance level.

pyramid: A 3-dimensional shape (polyhedron) formed by a (usually convex) polygon at the base with an enlargement between 0 and 1 as the centre of the polygon rises perpendicular to the base. the scale factor begins with 1 and the change is proportional to the distance the centre is away from the base, eventually reaching a scale factor of zero.

pyramidal: Of or related to the shape of a pyramid.

Pythagoras' theorem: A theorem in geometry that states that the square of the length of the hypotenuse equals exactly the sum of the square of the lengths of the other 2 sides in a triangle with a right angle.

Pythagorean triple: A set of 3 positive integers which can be exactly the sides of a right-angled triangle. There are infinitely many Pythagorean triples even if we exclude multiples of Pythagorean triples.

Common Pythagorean triples include 3, 4, 5 and 5, 12, 13 and others can be generated using the following rule: Using positive integers and t with s< t, calculate legs x and y and hypotenuse z as follows: x = 2ts, y = t^2 – s^2, and z = t^2 + s^2.

Pythagorean identities: The trigonometric identity that states that the sum of the square of the sine and cosine must always be exactly one regardless of the argument for the 2 trigonometric functions (although the argument must be the same for the 2 functions).